Academic Journal of Applied Mathematical Sciences
Online ISSN: 2415-2188
Print ISSN: 2415-5225
Print ISSN: 2415-5225
Quarterly Published (4 Issues Per Year)

Archives
Volume 6 Number 6 June 2020
On Properties of Derivations in Normed Spaces
Authors: Benard Okelo
Pages: 77-79
DOI: doi.org/10.32861/ajams.66.77.79
Abstract
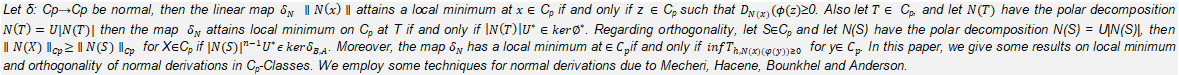
Computatıonal Algorıthm for the Numerıcal Solutıon of Systems of Volterra Integro-Dıfferentıal Equatıons
Authors: Falade Kazeem Iyanda ; Tiamiyu Abd`gafar Tunde
Pages: 66-76
DOI: doi.org/10.32861/ajams.66.66.76
Abstract
In this paper, we employ variational iterative method (VIM) to develop a suitable Algorithm for the numerical solution of systems of Volterra integro-differential equations. The formulated algorithm is used to solve first and second order linear and nonlinear system of Volterra integrodifferential equations which demonstrated a good numerical approach to overcome lengthen computational and integral simplification involves. Moreover, the comparison of the exact solution with the approximated solutions are made and approximate solutions p(x) q(t) proved to converge to the exact solutions p(x) q(t) respectively. The results reveal that the formulated algorithm are simple, effective and faster than analytical approach of solving Volterra integro-differential equations.
Spectral Features of Systems With Chaotic Dynamics
Authors: Perevoznikov E. N.
Pages: 58-65
DOI: doi.org/10.32861/ajams.66.58.65
Abstract
Using the Lorentz model and Hamiltonian systems without dissipation as an example, spectral methods for analyzing the dynamics of systems with chaotic behavior are considered. The insufficiency of the traditional approach to the study of perturbation dynamics based on an analysis of the roots of the classical spectral equation is discussed. It is proposed to study nonlinear systems using the method of constructing spectral equations with different eigenvalues, which allows one to take into account the randomness and multiplicity of states. The spectral features of instability and chaos for systems without dissipation are shown by the example of short-wave perturbations of a flow of a weakly ionized plasma gas.



