Academic Journal of Applied Mathematical Sciences
Online ISSN: 2415-2188
Print ISSN: 2415-5225
Print ISSN: 2415-5225
Quarterly Published (4 Issues Per Year)

Archives
Volume 6 Number 7 July 2020
Statistical Measures of Location: Mathematical Formula Versus Geometric Approach
Authors: ADENIRAN Adefemi Tajudeen ; OJO Johnson Funminiyi ; FAWEYA Olanrewaju ; BALOGUN Kayode
Pages: 145-152
DOI: doi.org/10.32861/ajams.67.145.152
Abstract
Graphical method and mathematical formula are the two approaches for estimating measures of location. Understanding of many instructors of introductory statistics classes are: mean cannot be graphically determined and numerical (formula) approach is more precise than geometrical technique. Contrary to their understanding, this study estimate mean of a dataset geometrically (from histogram) by determining the centroid of histogram drawn from such data set. In addition, we also make known that mathematical formulas for mean, median and mode were derived geometrically (either from ogive or histogram). Finally, the research illustrated the two techniques with a survey data and established that the two approaches produce same results.
Bi-Periodic Pell Sequence
Authors: S. Uygun ; H. Karataş
Pages: 136-144
DOI: doi.org/10.32861/ajams.67.136.144
Abstract
In this study, we introduce a new generalization of the Pell numbers which is called bi-periodic Pell sequences. We then proceed to find the Binet formula as well as the generating function for this sequence. The well-known Cassini, Catalan and the D’ocagne’s identities as well as some related binomial summation and sum formulas are also given. The convergence properties of the consecutive terms of this sequence is also examined.
Time-Dependent Flow of a Couple Stress Fluid in an Elastic Circular Cylinder with Application to the Human Circulatory System
Authors: T. S. L. Radhika ; T. Raja Rani ; A. Karthik
Pages: 126-135
DOI: doi.org/10.32861/ajams.67.126.135
Abstract
In this paper, we developed a mathematical model for blood flow in the human circulatory system. This model presumes blood to be a couple stress fluid, its flow to be pulsatile, and the artery an elastic circular pipe whose radius is assumed to vary with transmural pressure. The governing differential equation for the flow velocity is time-dependent and has been solved using the homotopy perturbation method. This velocity has been used to estimate the elastic modulus E of the artery, which is a measure of its stiffness and an important metric used by clinical practitioners to understand the state of the cardiovascular system. In this work, the radial artery has been considered and a limited set of experimental data, available for four cases, has been taken from the published literature to validate the model. While the experimental values of elastic modulus reported in literature lie in the range 2.68 1.81 MPa.s, those estimated through the proposed model range from 3.05 to 5.98 MPa.s, appearing to be in close agreement.
Study of MHD Heat and Mass Transfer Flow for Hall and Ion-Slip Currents Effects in High Porosity Medium and Revolving System
Authors: Md. Delowar Hossain ; Md. Abdus Samad ; Md. Mahmud Alam
Pages: 100-125
DOI: doi.org/10.32861/ajams.67.100.125
Abstract
In high porosity medium and revolving system the effects of ion-slip and Hall currents are studied on MHD heat and mass transfer flow. The non-linear coupled partial differential equations are determined using byl transformations and solve these equations employing finite difference method. Velocity, temperature as well as concentration profiles are studied for the concerned physical parameters and results are presented graphically. Due to the Hall and ion-slip parameters, Eckert number, and porosity parameter the velocity profiles are pronounced while it is declined for the effects of magnetic parameter, Prandtl number. Also the magnetic parameter enhances the temperature profiles. On the other hand, the temperature (concentration) profile decreases (increases) for the increasing effect of Prandtl number (Soret number). The rate of changes of velocity, temperature and concentration profiles are also presented graphically.
Positive Rational Number of the Form 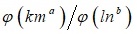
Authors: Hongjian Li ; Pingzhi Yuan ; Hairong Bai
Pages: 93-99
DOI: doi.org/10.32861/ajams.67.93.99
Abstract
Let 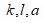 and
and 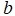 be positive integers with
be positive integers with 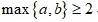 . In this paper, we show that every positive rational number can be written as the form
. In this paper, we show that every positive rational number can be written as the form 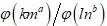 , where m,n∈N if and only if
, where m,n∈N if and only if 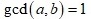 or
or 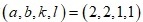 . Moreover, if
. Moreover, if 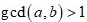 , then the proper representation of such representation is unique.
, then the proper representation of such representation is unique.
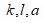 and
and 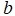 be positive integers with
be positive integers with 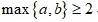 . In this paper, we show that every positive rational number can be written as the form
. In this paper, we show that every positive rational number can be written as the form 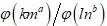 , where m,n∈N if and only if
, where m,n∈N if and only if 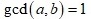 or
or 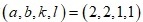 . Moreover, if
. Moreover, if 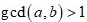 , then the proper representation of such representation is unique.
, then the proper representation of such representation is unique.
On the Positive Pell Equation 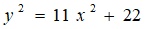
Authors: N. Thiruniraiselvi ; M. A. Gopalan
Pages: 85-92
DOI: doi.org/10.32861/ajams.67.85.92
Abstract
The binary quadratic equation 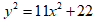 representing the hyperbola is studied for its non-zero distinct integer solutions. A few interesting properties among the solutions are presented. Employing the integer solutions of the equation under consideration, integer solutions for special straight lines, hyperbolas and parabolas are exhibited.
representing the hyperbola is studied for its non-zero distinct integer solutions. A few interesting properties among the solutions are presented. Employing the integer solutions of the equation under consideration, integer solutions for special straight lines, hyperbolas and parabolas are exhibited.
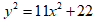 representing the hyperbola is studied for its non-zero distinct integer solutions. A few interesting properties among the solutions are presented. Employing the integer solutions of the equation under consideration, integer solutions for special straight lines, hyperbolas and parabolas are exhibited.
representing the hyperbola is studied for its non-zero distinct integer solutions. A few interesting properties among the solutions are presented. Employing the integer solutions of the equation under consideration, integer solutions for special straight lines, hyperbolas and parabolas are exhibited.
On The Ternary Quadratic Equation 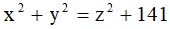
Authors: A. Vijayasankar ; Sharadha Kumar ; M. A. Gopalan
Pages: 80-84
DOI: doi.org/10.32861/ajams.67.80.84
Abstract
This article concerns with the method of determining different solutions in integers to 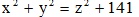 by reducing it to
by reducing it to 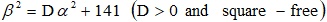 through employing transformations. A special case has been illustrated along with the corresponding properties. Also, given an integer solution, a process of obtaining sequence of integer solutions based on its given solution is exhibited.
through employing transformations. A special case has been illustrated along with the corresponding properties. Also, given an integer solution, a process of obtaining sequence of integer solutions based on its given solution is exhibited.
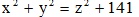 by reducing it to
by reducing it to 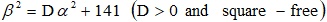 through employing transformations. A special case has been illustrated along with the corresponding properties. Also, given an integer solution, a process of obtaining sequence of integer solutions based on its given solution is exhibited.
through employing transformations. A special case has been illustrated along with the corresponding properties. Also, given an integer solution, a process of obtaining sequence of integer solutions based on its given solution is exhibited.



